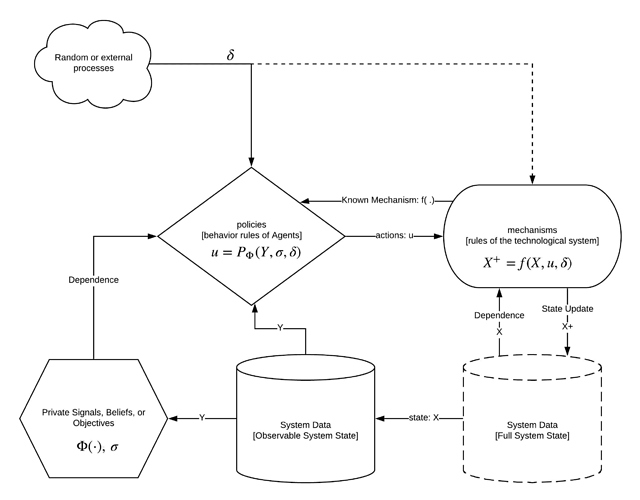
Since we are interested in modeling social and economic systems we are constantly asking what our agents will do. In order to ask this question it is first important to understand how a dynamic (or differential game) differs from a one shot game. A dynamic game has a persistent, potentially not totally observable state we call X.
When an agent takes an action we call that action u and the new state of the system is X^+ = f(X, u) where f:\mathcal{U}\times \mathcal{X}\rightarrow \mathcal{X} is a function, also called a mechanism, defining how that action changes the state. Here \mathcal{U} is the set of actions the agent is allowed to take and \mathcal{X} is the state space. In a simple system with one agent and one mechanism the agents sequence of actions would uniquely define a path through the state space, called a trajectory. An agent observing that they are at X_0 \in \mathcal{X} wishing to arrive at point X^* \in \mathcal{X} could chart a course of actions u_0,..., u_t \in \mathcal{U} such that they can expect to arrive at X_t =X^*. This is the canonical description of an open loop or non-feedback controller. In practice, the moment perturbations \delta are introduced, or there are other agents mutating the state but with goals not aligned with the original agent, it quickly becomes clear that our agent may never reach X^*.
If we suppose for a moment that our agent’s desire to be at X^* can be encoded as a private desire for the system to in state \sigma_t at any time t and their desire is encoded by an objective to \min \Phi where
Given a simple definition for the mechanism
it is possible to define a feedback controller to define the agents actions according to its own goals. If \sigma is constant and there is no noise then our agent can choose
In this case the answers can be computed closed form and implemented directly. If |\sigma - X_t|<1 then choose u_t = \sigma - X_t, otherwise if u_t = \hbox{sign}(\sigma-X_t) taking the largest allowable increment in the desired direction. Deriving control rules works even after injecting uncertainty \delta and hiding parts of the state. That is only allowing our agent to observe Y\subset X.
The dynamics start to get complex when there is state-feedback in the incentives, multiple mechanisms f_1, f_2,... and/or many agents interacting concurrantly with the same system. At this point we can define strategies for agents but those agents abilities to achieve their goals are uncertain. In some cases those agent’s goals may be unbounded, such as maximizing profit. This means that outcomes are determined as much by the interactions between the agents as they are by the individual agents strategies. In the case of multiscale systems the system itself may have adaptive properties.
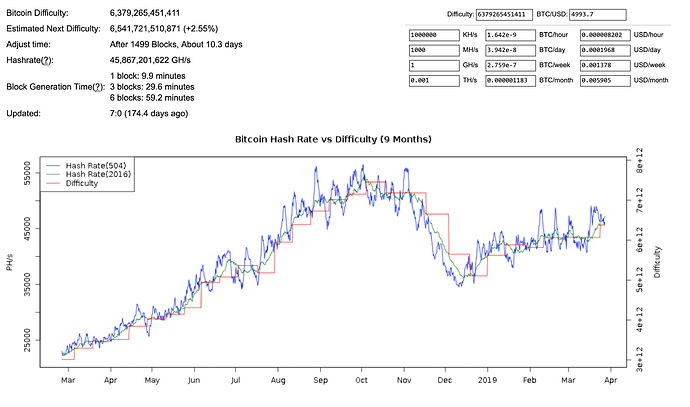
One such case is the Bitcoin network. If the agents are Bitcoin miners and their actions involve buying and operating mining hardware and their object is to make profit by mining blocks and collecting rewards, then the changes to the mining difficulty represent system level adaptivity in response to the aggregate behavior of the miners.
Source: https://bitcoinwisdom.com/bitcoin/difficulty
Looking at the aggregate system dynamics hides the nuances of the individual invest decisions and outcomes of all of the miners whose actions gave rise to these dynamics as well as that systems coupling with the secondary market for bitcoin, and the halving scheduling for Bitcoin mining rewards. There is forthcoming research on Bitcoin as a multi-scale game coming out of the Vienna CryptoEconomics institute.
More broadly, as the systems become more complex the behavioral models u_t = P(Y_t, \sigma_t, \delta) can be approached one of three ways:
- Agents behavior functions P(\cdot) can be encoded with Heuristic strategies derived from game theoretic, psychological decision sciences and/or behavioral economics literature.
- Agents behavior functions P(\cdot) can be machine learned from past data where the feature space is some characterization of the agent and system states, and the labels are the actions u taken.
- Agents can also have inherently adaptive strategies by encoding them as reinforcement learning agents who will learn to do whatever they can to achieve their goals within the bounds of the action space \mathcal{U}. In this case, P(\cdot) is itself time varying.
Models of all three types can be implemented in cadCAD; it is even possible for all of them to be used in the same model. I am looking forward to seeing this area of research pursued further as Bitcoin in particular has relatively simple dynamics and a 10 year history from which to draw data.