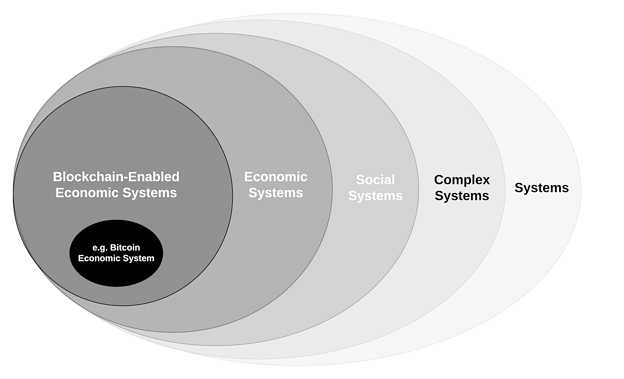
A Working Taxonomy of Systems Concepts
Charles Rice and Michael Zargham
A system is a group of interacting or interrelated entities that form a unified whole. A system is delineated by its spatial and temporal boundaries, surrounded and influenced by its environment, described by its structure and purpose, and expressed through its functioning. Systems are the subjects of study of systems theory.
A complex system is a system where the behavior of the whole within a given environment cannot be understood directly by understanding the behavior of the parts and the environment as separate additive entities. Rather, the system’s behavior is deeply dependent on the relations among the parts.
Systems that are “complex” have distinct properties that arise from these relationships, including:
- Non-linearity: the output of a complex system is greater than the sum of its parts;
- Emergence: the behavior of a complex system cannot be understood simply by looking at its components;
- Spontaneous order: the apparent chaos of a complex system produces order or stability without outside imposition;
- Adaptation: systemic behavior alters when it alteration finds, responding to change to aid the success of the system; and,
- Feedback loops: some portion of the system’s output becomes fresh input for the system.
In practice, complex systems exhibit unintuitive behaviors when they exist. Because complex systems appear in a wide variety of fields, the commonalities among them have become the subject of their own independent area of research. In many cases, it is useful to represent such a system as a model.
A model is a graphical, mathematical (symbolic), physical, verbal representation, or otherwise simplified version of a concept, phenomenon, relationship, structure, system, or aspect of the real world. The objectives of a model include:
(1) Facilitating understanding by eliminating unnecessary components,
(2) Aiding decision making by simulating ‘what if’ scenarios, and
(3) Explain, controlling, and predicting events on the basis of past observations.
Since most interesting objects and phenomena are both too complicated (they have numerous parts) and too complex (those parts are densely interconnected) to be understood in their entirety, a model contains only those features that are of primary importance to the model maker’s purpose.
Models can be broken down further into special types. A formal model is a model in which the description of the system is complete and unambiguous. It has well-formed syntax and semantics, such that it is amenable to systematic (usually automatable) processing and analysis subject to logical rules. It is based on rigorous methods and formats; it often enables analysis of the described system. A mathematical model is a special type of formal model that describes a system using mathematical concepts, symbols, and language. A computational model is a special type of a mathematical model which is expressed in a programming language. It allows the analyst to run simulations and backtest against data.
A quick aside on the nature of models and modeling.
-
Computational models are used extensively to explore complex systems because complex systems exhibit both non-ergodicity and non-linearity. Both non-ergodicity and non-linearity limit our capacity to extrapolate our past observations about a system’s past behavior into predictions about future behavior. Understanding the boundaries of our models is paramount to using them properly.
-
Models are subjective. Framing and modeling choices directly affect the conclusions an analyst or engineer reaches when using them. This is true of all fields and places an onus on the systems engineer to make choices which improve the usefulness of the models, even at the cost of precision. Models should be as simple as possible but no simpler.
-
While there is no optimal model per se, it is not fair to say all models are equal. In practice, a model should be judged by its usefulness, where usefulness is relative to some desired end. A model is useful when its application in the manner described above facilitates the operation and governance of the economic system in accordance with its goals.
-
Some models may become standard for certain situations and using them is considered best practice when there are well documented conditions under which the model is useful and the procedure for applying the model is standardized to the extent that the analyst need not directly revisit the model, but nonetheless relies on the validity of its underlying assumptions.
If we integrate a computational model with near real-time data from an implemented system, we create a digital twin of that system that aids the operations and governance of that implemented system. Digital twins support automated operations and human governance mechanisms, increasing visibility into the systemic effects of using specific instruments to change the system’s behavior.
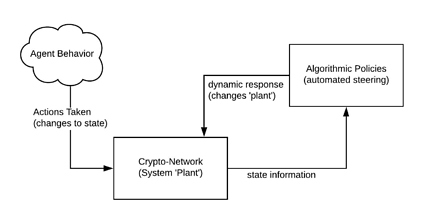
One of the primary subjects of any kind of model are systems that may be self-regulating to some degree. This breed of system is called an automated or autonomous system. An automated system entails a closed feedback loop between a computational system and another system under the computational system’s control that dynamically enforces a set of rules to drive a particular system behavior. The goals and behavior of agents are extrinsic to the automated system. Decentralized network software provide an automated system. (See Fig 1. Below)
Fig 1. A simple visual model of an Automated System
A closed feedback loop at a sufficiently high level of abstraction as to require no additional inputs in order to act is an autonomous system. The goals and behaviors of an autonomous system are intrinsic. (See Fig 2. Below)
Fig2. A simple visual model of an autonomous system